Предлагаемый в данной работе метод предназначен для автоматизации быстрого обнаружения основных тенденций связи пары переменных. Исходными данными для анализа является совокупность объектов, описанных двумя переменными Х и Y. Метод состоит в поиске такого дихотомического ("черно-белого") разбиения значений этих переменных, чтобы четырехклеточная таблица их сопряженности была максимально контрастной. Черно-белым мы называем этот вид анализа потому, что прежде всего мы пытаемся разделить совокупность объектов по каждой из переменных на 2 группы, содержательно отражающие два полюса в значениях переменных - "богатые-бедные", "старые-молодые", "должности прибыльные-неприбыльные" - без полутонов. Не ограничиваясь поиском контрастов, с использованием статистического моделирования мы проверяем устойчивость полученной группировки; неустойчивость группировки значений переменных дает полутона.

---

¹ Работа поддерживается Российским гуманитарным научным фондом, проект № 95-06-17638. Программная реализация метода на алгоритмическом языке С была произведена Н.Ю.Смирновой на основе подготовленного автором макетного варианта программы на языке BASIC. В этой реализации участвовали также В.С.Костин и Ю.Г.Корнюхин, обеспечив ряд сервисных возможностей. Автор благодарен указанному коллективу за проделанную работу и полезные обсуждения.

---

Ключевые слова: контрастность таблицы сопряженности, статистическое моделирование, устойчивость группировки, количественные и неколичественные переменные, "черно-белый" анализ, критерий дихотомического группирования.

Введение

Традиционно для исследования связи между парой переменных используются: критерий хи-квадрат - для исследования связи номинальных переменных; дисперсионный анализ - для исследования связи количественной и неколичественной переменных; коэффициент корреляции - для изучения взаимосвязи между количественными переменными; tau-b и tau-c Кендалла для ранговых переменных; кроме того применяется также ряд других критериев оценки связи ранговых переменных и ранговых и номинальных переменных, однако указанные наиболее популярны [I]. Значимая по этим критериям связь может служить поводом для содержательного исследования таблиц или полей рассеяния данных, либо подтверждением точными методами обнаруженной закономерности.

Необъятность таблиц стимулировала появление множества методов исследования таблиц сопряженности [2-8]. Эти методы позволяют выявить соответствия и связи по таблицам сопряженности, но не всегда дают возможность быстро определить основную тенденцию взаимосвязи переменных.

Предлагаемый в данной работе метод предназначен для автоматизации быстрого обнаружения основных тенденций связи пары переменных. Исходными данными для анализа является совокупность объектов, описанных двумя переменными Х и Y. Метод состоит в поиске такого дихотомического ("черно-белого") разбиения значений этих переменных, чтобы четырехклеточная таблица сопряженности агрегированных переменных была максимально контрастной. Здесь мы пытаемся разделить совокупность по каждой из участвующих переменных на 2 группы, содержательно отражающие два полюса в значениях переменных - "черное-белое", "богатые-бедные", "старые-молодые", "должности прибыль ные-неприбыльные". Характерно, что здесь происходит группировка одновременно по двум переменным. Исследование устойчивости позволяет сделать вывод: насколько достоверно проведена классификация значений,

Пример 1. Интуитивный черно-белый анализ связи денежного душевого дохода и профессионального образования.

Для демонстрации подхода мы используем анкетные данные социологического исследования "Первые итоги реформы", проведенного ИЭиОПП СО РАН в 1993 г. в Новосибирской области. В исследовании изучались социальные результаты реформ, проводимых в России.

Продемонстрируем "черно-белый" анализ связи переменных "профессиональная подготовка-доходы", сделанный без привлечения математического аппарата.

Можно предположить, что люди, имеющие более высокое образование, имеют шансы получать большие доходы. В соответствии с "черно-белым" подходом в качестве способа проверки этой гипотезы, воспользуемся таблицей сопряженности между дихотомическими переменными "душевой доход" (0 - низкий доход и 1 - высокий доход) и "профессиональная подготовка" (0 - низкая и 1 - высокая).

Где же граница высокого душевого дохода и образования? Чаще всего исследователь определяет эту границу интуитивно. В частности, высоким доходом можно считать доход выше среднего (по данным обследования средний денежный душевой доход составлял 5300 руб при максимальном - 80000 руб., минимальном - 6,5 руб.¹ и стандарт-

---

¹ Приведенные цифры соответствуют ценам 1993 года.

---

ном отклонении, равном 5400), высоким образованием -среднее специальное и высшее. Табл.1 - таблица сопряженности таких переменных, полученная на данных обследования "Первые итоги реформы".

СВЯЗЬ ПРОФЕССИОНАЛЬНОЙ ПОДГОТОВКИ С ДУШЕВЫМ ДОХОДОМ, ИНТУИТИВНАЯ ГРУППИРОВКА (АБСОЛЮТНЫЕ ЧАСТОТЫ, ПРОЦЕНТЫ ПО СТРОКЕ И ПО СТОЛБЦУ)

Таблица 1.

Душевой доход	Профессиональн. подготовка
	Невысокая	Высокая	Итого
Ниже среднего (менее 5300)	465 62.8% 81.3%	276 37.2% 57.1%	741 70.2%
Выше среднего (не менее 5300)	107 34.1% 18.7%	207 65.9% 42.9%	314 29.8%
Итого	572 54.2%	483 45.8%	1055 100.0%

 

Табл.1 весьма контрастна. Для того чтобы охарактеризовать эту контрастность, достаточно рассмотреть смещения долей в левой верхней ячейке этой таблицы в сравнении с другими ячейками и смещения частоты в этой ячейке по сравнению с ожидаемой в условиях независимости:

- если в целом по совокупности доходы ниже среднего имеют 70,2% респондентов, то среди респондентов с невысоким уровнем профессиональной подготовки их 81,3%;

- если в целом по совокупности невысокой профессиональной подготовкой обладают 54,2% респондентов, то среди респондентов с низким уровнем доходов их 62,8%;

- еще более разительно отличие между группами: доля "бедных" среди "малообразованных" и их доля среди "образованных" равны соответственно 81,3% и 57,1% ; доли "малообразованных" среди "бедных" и "богатых" равны 62,8% и 34,1% - разница почти 29%;

- в условиях независимости пропорции "бедных" и "богатых" среди "малообразованных" должны сохраняться, поэтому в среднем ожидается частота 572*(741/1055)=401,8, тогда смещение составляет 465-401,8=63,2.

Возникают вопросы:

- каким критерием контрастности следует воспользоваться и нельзя ли подобрать группировку по переменным, еще ярче подчеркивающую зависимость;

- как группировать значения для различных типов шкал переменных;

- насколько устойчивы результаты группирования?

Дихотомия для разных типов шкал.

Пусть значениям переменной Х (или Y) соответствует разбиение совокупности объектов на непересекающиеся классы объектов r={r₁,...,r_l}. Дихотомическое группирование состоит в объединении этих классов в разбиение R = {R₀,R₁}. При этом достаточно определить только одну группу значений переменной, которым соответствует класс R₀, класс R₁ составят остальные объекты.

Значения номинальной переменной не упорядочены, поэтому группировка по номинальной переменной не подчиняется какому либо правилу:

(1)

где М может быть любым подмножеством множества {1,...,l}

При группировании значений ранговых или количественных переменных целесообразно объединять только

группы рядом стоящих значений - интервалировать, поэтому

Особый класс представляют собой переменные, имеющие "кольцевую" структуру множества значений: наименьшее и наибольшее значения считаются совпадающими или близкими [10].

Примером таких переменных может служить время суток: 0 часов совпадают с 24 часами. Вторым примером может быть возраст индивидуума, рассмотренный с точки зрения возможности их привлечения к общественному труду. Глубокие старики и малые дети с этой точки зрения одинаково бесполезны. Здесь целесообразно в качестве R1 брать интервал значений, в общем случае не начинающийся с первого значения

Критерий дихотомического группирования. Контрастность таблицы.

Пусть значения каждой из переменных Х и Y сгруппированы в два класса и представлены разбиениями Rx и Ry. Для исследования значимости связи Rx и Ry изучается таблица частот

||F_ij||, I=0,1; j=0,l (4) в которой индексы i и j соответствуют классам Rx и Ry.

Существует множество коэффициентов, характеризующих связь дихотомических переменных: перекрестное отношение, коэффициент Юла, коэффициент коллигации и др. [8, II]. Для измерения значимости связи наиболее целесообразно использование точного критерия Фишера для малых выборок и Z-статистики отклонения частот для больших

выборок, основанных на гипотезе независимости. Первоначально мы пытались использовать именно последний критерий, однако перебор значений Z-статистик при поиске оптимального группирования из-за множественных сравнений сводит на нет их статистические свойства, а сложность критерия не позволяет построить эффективный алгоритм его оптимизации. Поэтому мы отказались от этого критерия и пользуемся более простым показателем - смещением элемента F₀₀ от его ожидаемого в условиях независимости значения Е₀₀.

Для формулировки показателя будем пользоваться обычными обозначениями:

F..j=F_0j+F_1j, F_i. = F_i0 + F_il и F..= F₀₀+F₁₀+F₀₁+F₁₁. (5)

При таких обозначениях ожидаемые значения элементов таблицы выражаются следующим образом:

E_ij=F_i.*F._j/N, (6) где N - число объектов в изучаемой совокупности.

Смещения элементов имеют вид

S_ij=F_ij-E_ij. (7)

Эти смещения и характеризуют контрастность таблицы. Ясно,что

S₀₀=-S₀₁=-S₁₀=S₁₁. (8)

Поэтому, для получения контрастной таблицы надо максимизировать абсолютную величину S₀₀.

Составляющие смещения.

Теперь вспомним, что Rx и Ry получаются из Х и Y, а таблица сопряженности (4) получается из таблицы сопряженности ||N_ij||, где индекс i = 1..т соответствует значениям X, а индекс j = l..n - значениям Y. Для этой матрицы также определяются ожидаемые частоты e_ij=N_i.N._j./N, где N_i. и N.j -маргинальные частоты (суммы элементов по строкам и по столбцам соответственно), и смещения r_ij=N_ij-e_ij.

Утверждение 1. Пусть Мх - множество значений X, которые соответствуют нулевому классу R_x - R_x0; My - множество значений Y, которые соответствуют нулевому классу r_y - R_y0. Тогда

Действительно,

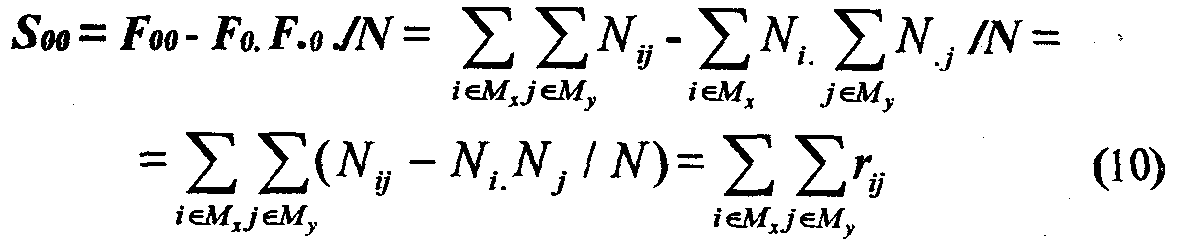
Таким образом, смещение S₀₀ представляет собой сумму смещений r_ij частот для значений i и j, где i u j соответствуют нулевым классам разбиений R_x0 и R_y0.

Обозначим r=||r_ij||, i=1,...,m; j=1,...,n матрицу отклонений от ожидаемых частот; I_х=(I_x1 ,..., 1_xm) и I_y=(I_y1 ,...,I_yn) -

индикаторные векторы, элементы I_x1, (I _уj ) которых.равны

нулю или единице, если i (j) принадлежат R_x0 (R_y0) или R_x1 (R_y1) соответственно. Критерий принимает "алгебраический" вид:

S₀₀ = S₁₁ = I_x r I_у (11)

Таким образом, задача поиска "черно-белого" деления значений переменных X и Y состоит в поиске максимума абсолютной величины смещения S₀₀ как функции на множестве булевых векторов I_х и Iy .

В зависимости от вида дихотомии эти булевы векторы могут иметь различную структуру, в частности:

01001100	номинальный тип - нули свободно чередуются единицами;
00001111	ранговый тип - в начале вектора нули, в конце - единицы;
11100011	кольцо - нули составляют интервал

 

Схема 1. Возможные виды булевых векторов, характеризующих дихотомию по переменным различного типа.

Алгоритмы

Максимизацию |S₀₀| необходимо проводить при всех сочетаниях типов переменных Х и Y.

Обозначим G(X) - число дихотомических группировок, которое можно получить группированием переменной X. Вообще говоря, при оптимизации S₀₀ необходимо проверить G(X)G(Y) двумерных группировок.

Ясно, что для рангового признака G(X) = n_х-1, для кольцевого G(X) = (п_х-1) (п_х-2)/2 и для номинального G(X)

= 2^nx-1, где n_х - число значений признака Х .

Опыт показывает, что в случае, когда Х и У - ранговые переменные или переменные типа "кольцо", практически всегда можно провести полный перебор всех G(X)G(Y) возможных сочетаний разбиений по переменным Х и У.

В остальных случаях нам помогает простой алгоритм получения оптимального разбиения по номинальной переменной, если по другой переменной разбиение известно, который основывается на следующем утверждении.

Утверждение 2. Пусть фиксировано разбиение по У, и

пусть р_i0 = E_jeMy r_ij, тогда оптимальное разбиение по Х определяется

М_х={i | р_i0 > 0}. (12)

Действительно, поскольку

легко можем убедиться, что максимум S₀₀ достигается при М_х = { i| p_i0 > 0 } и для нахождения оптимального М_х достаточно определить знаки p_i0, i=1,...m.

Таким образом, благодаря аддитивности показателя S₀₀, оптимизация для номинального Х и рангового или кольцевого Y не представляет сложности: она состоит в полном переборе всех группировок по Y, определении оптимальной группировки по Х для каждой из этих группировок и выборе оптимальной пары М_х и M_y.

С учетом этого же утверждения при номинальных Х и Y и малом числе значений Y реально провести оптимизацию, проводя полный перебор всех классификаций по Y, для каждой из них максимизируя S₀₀ по группировкам по X.

В случае невозможности в реальном времени провести полный перебор таких классификаций нами проводится локальная оптимизация за счет последовательных перемещений значений Y из одного класса разбиения в другой с оптимизацией разбиения по X. Перемещения производятся до тех пор, пока происходит рост оптимизируемого функционала. Подобные алгоритмы локального перебора описаны в [11, 12].

Устойчивость и полутона в чёрно-белом анализе. Метод BOOT STRAP.

Повторный сбор данных и их обработка может разрушить ясную и четкую картину, полученную в результате черно-белого анализа. Для выяснения степени устойчивости полученных дихотомий мы используем метод BOOT STRAP [13]. Ранее этот метод был применен нами для анализа структуры таблиц сопряженности, типологического анализа и анализа кластерной структуры [7, 9, 14] и оказался полезен и в данном случае.

В соответствии с этим методом предполагается, что данные репрезентативны, то есть двумерные распределения для каждой изучаемой таблицы соответствуют (или почти соответствуют) распределению генеральной совокупности. При этом предположении, извлекая с возвращением объекты (анкеты) из имеющейся совокупности и переписывая их в генерируемый массив данных, мы будем имитировать повторный сбор данных.

В каждом эксперименте генерируется выборка, объем которой совпадает с исходными данными. Так как производится выборка с возвращением, с извлечением новых объектов в исходной выборке данных не происходит изменения распределения. Сгенерированная же выборка будет иметь распределение, несколько отличающееся от распределения исходных данных. В этой сгенерированной выборке будут исходные данные, но часть объектов повторится несколько раз, часть - не встретится ни разу.

При работе алгоритма "черно-белого" анализа на сгенерированных данных часть значений класса R_x0 перейдет в R_x1 и наоборот, часть значений класса R_x1 перейдет в R_x0. To же самое касается классификации по Y.

В результате экспериментов каждому значению переменных Х (Y) будет приписываться относительная частота, с которой значение оказывалось в классе R_x1 (R_y1). Совокупность таких относительных частот может быть также выражена средним индикаторных векторов I_х и I_у, получаемых в экспериментах. Образно выражаясь, значения переменной Х (Y), во всех экспериментах попавшие в нулевой класс -"черные", значения, всегда попадающие в первый класс, -"белые", значения, для которых соответствующая относительная частота находится между нулем и единицей -"полутона". В выдаче программы в нашей реализации алгоритма устойчивость ("степень серости") выражена в процентах (цомножена на 100).

Корректировка в случае инверсии.

В действительности не важно, как обозначить класс разбиения совокупности по переменным Х или Y, нулевым или первым - все равно агрегированная таблица будет состоять из тех же самых ячеек, которые будут лишь переставлены. В частности, индикаторные векторы классификаций 01100110 и 10011001 можно считать эквивалентными.

Пусть А и В ноль-единичные векторы одинаковой размерности. Назовем вектор В инверсией вектора А, если нулевым компонентам А соответствуют единичные компоненты В, единичным компонентам - нулевые.

Если непосредственно следовать алгоритму, в статистическом эксперименте в принципе можно получить практически ту же классификацию значений переменной, что и на исходных данных, в которой лишь классы поменялись местами - нулевой стал первым, а первый - нулевым (то есть индикаторный вектор классификации стал инверсией индикаторного вектора для исходных данных). Таким образом здесь может быть получена ложная неустойчивость классификации.

Эта проблема касается лишь номинальных переменных, поскольку положение нулевого класса в ранговом признаке и признаке типа "кольцо" фиксируется соответственно в начале шкалы и в виде интервала внутри всего упорядоченного множества значений.

Обозначим T_x = (T_x1 ,..., T_xm) и Т_у=(Т_y1 ,...,Т_ym) индикаторные векторы, полученные алгоритмом в случайном эксперименте, U_x=(U_x1,...,U_xm) и U_y=(U_y1 ,..,U_ym) - их инверсии.

Вопрос состоит в том, что следует выбрать для оценм устойчивости, сам индикаторный вектор или его инверсию? Для решения этого вопроса мы рассматриваем близосп классификаций, порожденных индикаторными векторам! Т_х и U_x (Т_у и U_y), к классификации, полученной на исходные данных. Близость вычисляется по формулам

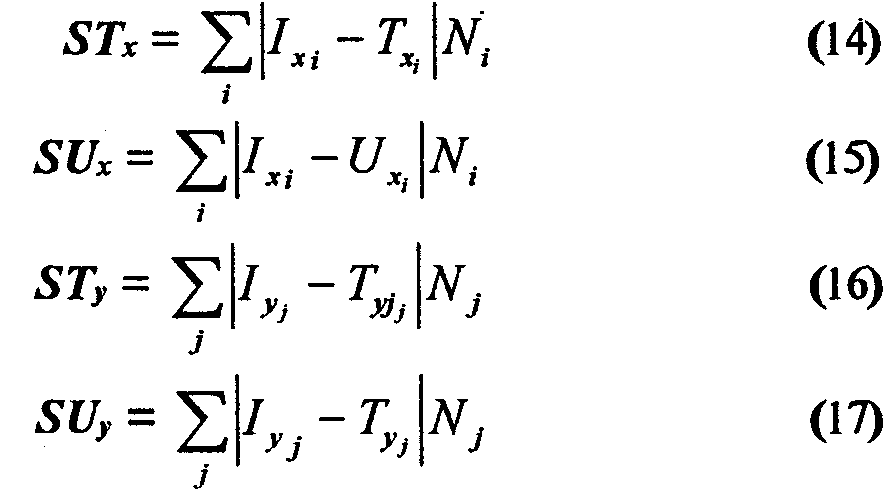
Если оказывается, что ST_x > SU_x , то для оценки устойчивости (полутонов) используется вектор U_x, в противном случае - вектор Т_х, аналогичный выбор происходит для оценки устойчивости по значениям Y.

Вообще говоря, этот подход не единственный. Можно проверять устойчивость, включая в экспериментах локальный алгоритм, можно при согласовании учитывать не только одномерные, но и двумерные распределения. В данной работе мы не ставили цели реализации и сравнительного исследования этих подходов.

Использование метода.

Вернемся к данным исследования социальных результатов реформ, проводимых в России.

Пример 2. Профессиональная подготовка и душевой доход. Здесь мы рассмотрим, чем отличается представленная выше интуитивная группировка (табл.1) от группировки, полученной с помощью описываемого метода, а также устойчивость этой группировки; переменная "Профессиональная подготовка" считается номинальной переменной, "душевой доход" - ранговой переменной.

Группировка по профессиональному образованию имеет следующий вид:

• нулевой класс: "нет профессионального образования" "курсы", "ПТУ, ФЗУ, РУ";
• первый класс: "среднее специальное", "высшее", "другое".

В отличие от интуитивной группировки (см. пример 1) к "высокообразованным" здесь присоединились респонденты, указавшие образование, не предусмотренное в списке подсказок ("другое", 7 респондентов). Таким образом здесь "компьютерная" дихотомия несущественно отличается от интуитивной.

Группировка по душевому доходу представлена интервалами:

• нулевой класс: менее 4500 руб.;
• первый класс: не менее 4500 руб.

Здесь граница смещена от величины среднего, дохода в сторону меньших доходов на 800 руб. (максимальный душевой доход равен 80000 руб, минимальный - близок к нулю, -он равен 6.5 руб).

СВЯЗЬ ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ С ДУШЕВЫМ ДОХОДОМ, ГРУППИРОВКА АЛГОРИТМОМ ЧЕРНО-БЕЛОГО АНАЛИЗА (АБСОЛЮТНЫЕ ЧАСТОТЫ, ПРОЦЕНТЫ ПО СТРОКЕ И ПО СТОЛБЦУ)

Таблица 2.

Душевой . ДОХОД	Профессиональное образование
	Низкий уровень образования	Высокий уровень образования	Всего
Низкий яоход (менее 4500)	405 (00) 66,6% 71,7%	203 (01) 33,4% 41,4%	608 57,6%
Высокий доход (не менее 4500)	160 (10) 35,8% 28,3%	287 (11) 64,4% 68,6%	447 42,4%
Всего	565 58,6%	490 41,4%	1055 100,0%

 

Если в примере 1 в клетке (низкий доход, низкий уровень образования) удалось добиться смещения Sov, равного 63.2, то в компьютерной классификации это смещение составляет 79.4. Таким образом, табл.2 более контрастна. Это же можно подтвердить, изучая смещения распределений по отношению к итоговым. В целом здесь, как и по табл.1, можно сделать вывод, что высокий уровень образования дает больше возможностей улучшить состояние семейного бюджета.

Устойчивость классификации по профессиональному образованию показана в табл.3, в которой графа "Степень серости" соответствует частоте попадания значений в класс 1. По всей видимости, классификация недостаточно надежна в отношении группы неимеющих профессионального образования (возможно, это молодежь, способная активно зарабатывать уличной торговлей, процветающей в России в год проведения обследования), а также в отношении группы с высшим образованием (вероятно, из-за несоответствия опыта прежней работы современным условиям). Первая группа 14 раз оказывалась в первом классе, вторая - 13 раз в нулевом классе.

 

УСТОЙЧИВОСТЬ КЛАССИФИКАЦИИ ПО ПРОФЕССИОНАЛЬНОМУ ОБРАЗОВАНИЮ

Таблица 3.

Проф. образование	курсы	ПТУ, ФЗУ, РУ	нет проф. образования
Степень серости	0%	4%	14%
Проф. образование	высшее	среднее специальное	другое
Степень серости	87%	100%	100%

 

Устойчивость классификации по душевому доходу представлена в табл. 4. Граница, разделяющая классы, принимала в экспериментах значения от 3600 до 5000. Таким образом, с точки зрения формального критерия интуитивно принятая в примере 1. граница 5300 руб. имеет слишком большое значение даже с учетом неустойчивости результатов.

УСТОЙЧИВОСТЬ КЛАССИФИКАЦИИ ПО ДУШЕВОМУ ДОХОДУ

Таблица4.

Душевой доход Степень серости	менее 3600 3600 3700 3725 3800 3900 4000 0% 6% 8% 10% 15% 21% 31%
Душевой доход Степень серости	4000 4050 4100 4109 4118 4150 4200 31% 43% 58% 58% 58% 58% 58%
Душевой доход Степень серости	4230 4250 4300 4350 4400 4450 4500 58% 60% 60% 65% 70% 77% 91%
Душевой доход Степень серости	4530 4600 4750 4900 5000 более 5000 91% 93% 94% 95% 99% 100%

Пример 3. Место работы и изменение материального положения. В этом примере агрегируемая таблица не столь необъятна, как в предыдущем примере, и позволяет рассмотреть не только агрегированные, но и агрегируемые таблицы, включая процентные распределения и остатки r_ij.

Реформа вызвала в различных слоях населения отрицательные и положительные реакции. В частности, эти реакции дифференцированы в группах населения, связанных с различными формами организации труда. В обследовании эта взаимосвязь отражается вопросами "Укажите Ваше основное место работы" и "Какие изменения произошли в Вашем материальном положении?". Связь соответствующих переменных представлена таблицей их совместного распределения (табл. 5). Обе переменные рассматриваются как номинальные. По этой таблице можно, в частности, обнаружить, что 35.1% респондентов, работающих в акционированных предприятиях, не почувствовали изменений в материальном положении, 51.9% - стали жить хуже; 23.9% работников государственных предприятий не заметили изменений, 65.1% - стали жить хуже; среди колхозников эти же цифры составляют 14.3% и 71.4%. Таким образом, уже по этой таблице видно, что труднее реформы проходят для государственных предприятий и колхозов, чем для акционированных предприятий.

Изучая различие распределений по строкам и столбцам, можно проводить множество подобных сравнений. Это интересно, но с определенного момента становится утомительным и однообразным. Что же дает в данном случае черно-белый анализ? В дихотомической группировке по переменной "изменение материального положения" нулевой класс объединяет ответы "изменений не произошло", "жить стало лучше" и "затрудняюсь сказать"; первый класс соответствует ответу "жить стало хуже" (табл. 6). Очевидны названия для классов этой классификации - "жить стало не хуже" и "жить стало хуже".

Следует обратить внимание на то, что первый класс классификации, полученной в результате группирования значений переменной "место работы", составляют основные старые формы организации труда - "колхоз" и "государственное предприятие", остальные виды мест работы (в основном новые формы организации труда) и значение "не работаю" этой переменной составляют нулевой класс.

Положительные смещения в блоке (11) и преимущественно положительные смещения в блоке (00) свидетельствуют о том, что респондентам, "работающим на предприятиях со старой формой труда" " жить стало хуже", чем в среднем по всей совокупности; респонденты, "место работы которых не связано со старой формой труда", находятся в лучшем положении.

 

Полутона в черно-белом анализе, полученные в результате 100 имитаций сбора данных и повторного анализа, представлены в вертикальной и горизонтальной графах табл.6 под названием "Степень серости". Как ранее было описано, это доли (в процентах) попадания значений переменных (строк или столбцов таблицы) в первый класс. При этом для нулевого класса абсолютная устойчивость означает относительную частоту 0%, для первого - 100%. Абсолютно устойчиво классифицируются значения "изменений не произошло" и "жить стало хуже" переменной "оценка изменений в материальном положении". Достаточно устойчиво принадлежит нулевому классу значение "жить стало лучше" и неустойчиво отнесение к нулевому классу значения "затрудняюсь сказать" (35 раз из 100 это значение уходило из нулевого в первый класс) - компьютер "сомневается" в правильной классификации этого значения.

 

СВЯЗЬ МЕСТА РАБОТЫ С ОЦЕНКОЙ ИЗМЕНЕНИЙ В МАТЕРИАЛЬНОМ ПОЛОЖЕНИИ. (СМЕЩЕНИЯ ОТ ОЖИДАЕМЫХ ЧАСТОТ, ЧЕРНО-БЕЛАЯ СТРУКТУРА, РЕЗУЛЬТАТЫ 100 ЭКСПЕРИМЕНТОВ ПО ИССЛЕДОВАНИЮ УСТОЙЧИВОСТИ)

Таблица 6.

	изменений не произошло	жить стало лучше	затрудн. сказать	жить стало хуже	тепень серости     1% 4% 5% 9% 16% 19% 24% 28%       68% 100%
акцион. предпр. кооперативы фермер, хоз-ва совмес. предпр. потреб.коопер. муниц. предпр. частное предпр. не работаю	(00) (00) (00) 17,16 -0,52 0,79 -0,21 2,36 0,61 1,17 0,76 -0,15 0,89 0 ,68 -0,19 0,68 1,04 0,42 -1,04 3,03 1,78 -0,49 1,28 0,56 2,95 -0,21 -1,94			(01) -17,43 -2,76 -1,78 -1,38 -2,14 -3,76 -1,35 -0,80
колхоз госуд. предпр.	(10) (10) (10.) -0,93 0,44 -0,34 -20,18 -8,85 -1,54			(11) 0,84 30,57
Степень 0% 4% 35% 100% серости

 

Относительно устойчиво отнесение к нулевому классу значений признака "место работы" "акционированное предприятие", "кооператив", "фермерское хозяйство", "совместное предприятие" (соответственно 1, 4, 5, 9 раз меняли класс); абсолютно устойчиво значение "государственное предприятие". Неустойчивы "потребительская кооперация", "муниципальное предприятие", "частное предприятие" и особенно неустойчивы "не работаю" и "колхоз" - здесь внутри блоков (00) и (10) наблюдается пестрая картина положительных и отрицательных смещений.

Вероятно, здесь возможен и более глубокий содержательный анализ результатов. Мы предоставляем читателю возможность подумать над этим вопросом.

Об интерпретации результатов чёрно-белого анализа.

На основании опыта применения метода в содержательном анализе результатов группирования можно сделать некоторые замечания.

Первое, что необходимо сделать после автоматического группирования, - сформулировать термины для названия нулевого и первого классов, отражающие содержательную суть выявленных полюсов. После проведения экспериментов появляются серые тона - значения полностью не относящиеся ни к одному полюсу. Следует ответить содержательно на вопрос, почему? Например, возможна формулировка: "ответ "затрудняюсь сказать" в оценке изменения материального положения не может быть прямым или косвенным образом четко связан с формой собственности предприятия, что, по-видимому, объясняет неустойчивость классификации соответствующего значения".

Нередко возможен вариант, когда один из "полюсов" -значение "не знаю", другой полюс - противоречивые ответы "знаю". Такой результат не всегда интересен. Здесь можно исключить из выборки часть объектов, соответствующих такому значению, и продолжать анализировать связь переменных по остальным значениям. Обобщением такого подхода может быть последовательный черно-белый анализ: последовательно анализируются и исключаются из рассмотрения те или иные значения.

Анкетная информация часто содержит неальтернативные вопросы, подобные вопросам "Что нравится в деревенской жизни?" и "Что нравится в городской жизни?". Здесь мы рассматриваем в качестве объекта (статисти

ческого наблюдения) пару ответов и получаем соответствующие таблицы сопряженности. Переменные считаются номинальными. Опыт показал, что техника анализа здесь такая же, как в обычном случае.

Заключение.

Основным преимуществом представленного средства анализа данных является простота и ясность результата. Простота схемы группирования позволяет быстро проводить вычисления, поэтому принципиально возможно использование точных алгоритмов, максимизирующих критерий. Возможна полноценная проверка значимости связи переменных, основанная на многократном перемешивании данных. Однако, простота нередко бывает чревата неприятными последствиями: дихотомическая схема группирования может скрыть мелкие нюансы взаимосвязи. Поэтому данный алгоритм целесообразно использовать в сочетании с другими методами.

ЛИТЕРАТУРА

1. Афифи А„ Эйзен С. Статистический анализ. Подход с использованием ЭВМ. М.:Мир, 1982.

2. Аптон Г. Анализ таблиц сопряженности. М.:Финансы и статистика, 1982.

3. Haberman Sh.J. Analysis of Qualitative Data. Volume 1. N.-Y., 1978.

4. Rehak J., Rehakova B. Analisa kontingencnich tabulek: dva akiadni typy uloh a znakomenkove schema//Sociologicky casopis, c.6. Praha, 1978.

5. Pleszczynska E; Szczesny W., Wisocki W. The Importance of Grade Methods in Multivatiate Statistical Analysis/Proceedings of 14th International Conference on Multyvariate Statistical Analysis (MSA'95). Warsaw, 1995. P.87-97.

6. ФлейсДж. Статистические методы для изучения таблиц долей и пропорций. М.:Финансы и статистика, 1989.

7. Ростовцев П.С., Смирнова Н.Ю., Корнюхин Ю.Г., Костин B.C. Анализ таблиц сопряженности неальтернативных призна-ков/Шрепринт 138. Новосибирск:ИЭиОПП СО РАН, 1995.

8. Ростовцев П.С. Статистическое согласование мер связи в анализе социально-экономической информации/УЭкономика и математические методы. Том 26. М., 1991.

9. Ростовцев П.С., Костин B.C. Автоматизация типологического группированил//Препринт 137. Новосибирск:ИЭиОПП СО РАН, 1995.

10. Лбов Г.С., Коттков В.И; Манохин А.Н. Об одном алгоритме распознавания в пространстве разнотипных признаков/УВы-числительные системы. Вып. 55. Новосибирск, 1976.

11. Миркин Б.Г. Анализ качественных признаков и структур. М.:Статистика, 1980.

12. Браверман Э.М., Мучник И. Б. Структурные методы обработки эмпирических данных. М.:Наука, 1983.

13. Efron В. Better bootstrap confidence intervals//.!. Amer. Statist. Ass., 1986. №81.

14. Ростовцев П.С. Значимость и устойчивость автоматической классификации - возможности исследования при анализе археологических данныхУ/Методы естественных наук в археологических реконструкциях. Часть 1. Новосибирск, 1995.

Выберите оценкуПлохоСойдетХорошоОтличноНевероятно!

Ваша оценка: Нет Средняя: 4 (1 голос)