А.О. Крыштановский. Ограничения метода регрессионного анализа
В статье рассматриваются некоторые проблемы, связанные с использованием регрессионного анализа в социологии. Обсуждаются ограничения, обусловленные неравенством дисперсий (гетероскедастич-ностью) и мультиколлинеарностью в регрессионных моделях. Предлагается несколько подходов к снижению последствий нарушения этих ограничений.
Ключевые слова: регрессионная модель, линия регрессии, коэффициент детерминации, фиктивные переменные, гетероскедастичность, коэффициент Спирмена, мультиколлинеарность.
Построение регрессионных моделей на сегодняшний день, несомненно, является наиболее широко применяемым методом многомерного статистического анализа социологических данных. За последние несколько лет более половины статей, анализирующих эмпирические данные, в таких американских социологических журналах, как American Journal of Sociology и American Sociological Review, основаны на использовании регрессионных моделей.
Достаточно распространены регрессионные методы и среди российских социологов, специалистов, использующих опросные методики. Вместе с тем многие особенности и ограничения регрессионных моделей обычно остаются вне сферы внимания исследователей, что, подчас, приводит к неточным, либо просто ошибочным результатам. В данной статье рассматриваются некоторые особенности использования регрессионных методов при анализе данных массовых опросов.
Проблема недостаточности одного уравнения
Традиционная модель множественного линейного регрессионного анализа подразумевает поиск показателей (обозначаемых X), определяющих значение отдельной количественной переменной, обозначаемой Y. Структура связи в данной модели предполагается линейной. Иными словами, ищется следующая форма зависимости:
Y=B0+B1*X1+B2*X2+....+Bn*Xn+U, (1) где U -так называемый остаточный член, фиксирующий ту часть информации Y, которая не объясняется иксами.
Регрессионный анализ показывает, во-первых, качество модели, то есть степень того, насколько данная совокупность иксов объясняет Y. Показатель качества называется коэффициентом детерминации R2 и показывает, какой процент информации Y можно объяснить поведением иксов. Во-вторых, регрессионный анализ вычисляет значения коэффициентов В, то есть определяет, с какой силой каждый из Х влияет на Y.
Методологическим недостатком такого подхода является то, что данная зависимость ищется единой для всей совокупности опрошенных респондентов. Иными словами, мы предполагаем, что для всех людей характер зависимости Y от иксов единый. В том случае, когда выборочная совокупность достаточно однородна, такого рода допущение имеет под собой определенные основания. Однако, если анализируются, скажем, детерминанты электоральных предпочтений на основе данных всероссийской выборки, допущение об однородности этих детерминант для чукотского оленевода и для московского профессора выглядит не очень убедительным.
Единая форма уравнения в этой ситуации сильно огрубляет реальную зависимость, качество модели неизбежно оказывается весьма низким, а смысл регрессионных коэффициентов, фиксирующих степень влияния иксов на Y, можно приравнять к пресловутому показателю "средней температуры по больнице".
Вполне очевидно, что гораздо разумнее строить отдельные модели для существенно различающихся между собой групп респондентов. Однако доведение такого подхода до логического завершения чревато опасностью полного релятивизма. Действительно, всегда можно найти более или менее убедительные аргументы в пользу того, что по анализируемой проблеме механизмы формирования оценок различны у женщин и мужчин, у горожан и сельских жителей, у инженеров и рабочих и т.д. и т.п. Следовательно, для каждой группы необходимо строить свою модель, что не очень конструктивно, поскольку количество таких моделей ограничивается лишь фантазией социолога по разбиению всей совокупности на отдельные группы.
Оказывается, однако, что есть определенные формальные критерии, позволяющие определять границы групп, для которых действуют одинаковые, либо различные механизмы. Рассмотрим такие критерии вначале на примере простейшей задачи.
В качестве зависимой переменной мы взяли придуманный нами в учебных целях индекс "степень зажиточности", измеряемый по количеству предметов долговременного пользования, которые есть у респондента в семье1: Задачей являлось определе-
1 Вопрос анкеты выглядел следующим образом:
ОТМЕТЬТЕ, ПОЖАЛУЙСТА, В ПРИВЕДЕННОМ НИЖЕ СПИСКЕ ВЕЩИ, КОТОРЫЕ ЕСТЬ В ВАШЕЙ СЕМЬЕ:
- 1 цветной телевизор
- 2 фотоаппарат
- 3 радио-часы
- 4 миксер
- 5 электродрель
- 6 стерео-, радиосистема
- 7 отдельный морозильник
- 8 микроволновая печь
- 9 видеомагнитофон
- 10 видеокамера
- 11 пылесос
- 12 домашний компьютер
- 13 пианино (фортепиано)
- 14 автомобиль, купленный новым
- 15 автомобиль, купленный подержанным
- 16 дача, дом на садовом участке
- 17 дом в деревне
- 18 участок, где Вы выращиваете овощи, фрукты
- 19 проигрыватель компакт-дисков
- 20 нет ничего из перечисленного
ние степени влияния возраста на этот индекс. Данные взяты из всероссийского социологического опроса, проведенного Всероссийским центром изучения общественного мнения (ВЦИОМ) в ноябре 1999 года по репрезентативной национальной выборке. Объем выборки - 2388 человек.
Сам индекс "зажиточности" - это просто сумма ответов респондента по каждой из отмеченных в вопросе 19-ти позиций. Естественно, что данный индекс фиксирует лишь количественный, но не качественный аспект "зажиточности", поскольку и Проигрыватель дисков, и автомобиль, и дача входят в этот индекс с одинаковым весом. Однако мы рассматриваем этот индекс исключительно как инструмент для демонстрации метода.
График зависимости индекса "зажиточности" от возраста приведен на рисунке 1. Представленная здесь регрессионная модель выглядит следующим образом:
"зажиточность"=5,97 - 0.049 * (возраст) (2) Качество полученной модели не очень высоко - коэффициент детерминации равен 0,097, но, с другой стороны, этот коэффициент значим с Р>0,999, с той же вероятностью значимы регрессионные коэффициенты и, если взглянуть на результаты оптимистически, то можно сказать, что возраст почти на 10% определяет степень зажиточности российского населений.
Построенная модель дает нам единый механизм влияния возраста на индекс "зажиточности" независимо от значения возраста. Другими словами, модель утверждает, что с увеличением возраста на 10 лет респондент в среднем теряет 0,5 вещи, независимо от того, 20 лет респонденту или 70. Однако жизненный опыт и здравый смысл подсказывают, что это, скорее всего, не так. Действительно, можно предположить, что в 20-40 лет респонденты скорее увеличивают количество вещей, а в пожилом возрасте, в силу сокращения доходов, уже начинают терять. Полученный же средний коэффициент - "минус 0,5 вещи за 10 лет", таким образом, вообще ни к кому не применим, это то усреднение, которое, фактически, ничего не описывает.
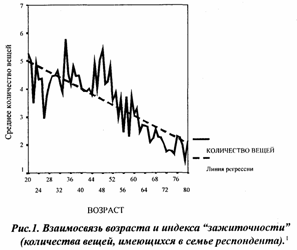
1 Из анализа были исключены респонденты младше 20 лет и старше 80. После такого исключения объем выборки составил 2233 респондента.
Проблема, которая следует из предыдущего рассуждения, следующая: если делить весь жизненный цикл респондента (с точки зрения "индекса зажиточности") на два этапа, то где находится это пороговое значение, где кончается один этап и начинается другой? Эту постановку проблемы можно перевести на язык регрессионной модели следующим образом. Если строить для двух совокупностей респондентов две регрессионные модели, то как определить, когда эти две модели отличаются друг от друга и где это отличие максимально?
Для решения этой задачи существует специальный статистический тест, называемый тестом Чоу. Он показывает, является ли значимым улучшение качества регрессионной модели после разделения выборки [1, с. 282-285]. Для этого используется F-статистика, вычисляемая следующим образом:
![]()
где Up - сумма квадратов остатков для единой модели;
UA - сумма квадратов остатков для первой модели;
UB - сумма квадратов остатков для второй модели;
k=l (в данном примере);
n - объем выборки.
Получаемая таким образом F-статистика имеет F-распределение с (k+1) и (n-2*k-2) степенями свободы и позволяет определить статистическую значимость улучшения объясняющей силы модели при переходе от одного уравнения к двум.
Таким образом, возвращаясь к анализируемому примеру, можно разделить возрастную шкалу на два интервала, построить для каждого из этих интервалов свою линию регрессии и с помощью теста Чоу определить, произошло ли улучшение качества модели. Проблема, однако, состоит еще и в том, как выбрать точку разбиения.
Действительно, можно разбить возраст на интервалы "20-25 лет" и "старше 25 лет" и получить, что тест Чоу значим. Можно предложить какое-либо другое разбиение и получить тот же результат (в ходе наших экспериментов с данной моделью оказалось, что почти любое разбиение дает значимые различия по тесту Чоу). Эта закономерность имеет положительную сторону. Она означает, что две отдельных линии регрессии почти всегда лучше описывают реальную ситуацию, чем одна единственная, и это, как представляется, немаловажный результат.
С другой стороны, мы не получаем ответа на вопрос, на какие же все-таки интервалы лучше разбить возрастную шкалу. Решение данной проблемы в свете вышеизложенного выглядит достаточно просто. Необходимо перебрать все возможные, разумные с социологической точки зрения, разбиения и взять то из них, которое дает наибольшее увеличение показателя качества модели, основываясь на F-статистике теста Чоу. В таблице 1 показаны значения F-статистики для нескольких предпринятых разбиений.
Для всех значений F-статистики в Таблице! число степеней свободы одинаково - (2,2229). Они (значения F-статистики) значимы на 0,1 % уровне и, поскольку число степеней свободы одинаково, мы можем сравнивать значения F-статистики между собой и выбирать максимальное. Как видно из таблицы, наилучшим разбиением являются интервалы "20-44 года", "45 лет и старше".
На рисунке 2 показана модель с двумя линиями регрессии при разбиении шкалы возраста на эти два интервала. Как же выглядят две полученные линии регрессии? Первая из них (для интервала возраста "20-44 года") дает значение коэффициента детерминации R2=0,002, которое соответствует незначимой (с Р>0,18) величине дисперсионного F-отношения. Иными словами, для респондентов из этого возрастного интервала нет значимого влияния возраста на значение индекса "зажиточности", и для них этот индекс - просто константа, равная 4,8.
Для второго интервала возраста (45 лет и старше) коэффициент детерминации R =0,172, регрессионная зависимость высоко значима и уравнение выглядит следующим образом' •
«зажиточность» = 8,97 - 0,097 * (возраст) (4) (0,4) (0,007)
ЗНАЧЕНИЯ F-СТАТИСТИКИ ДЛЯ РАЗЛИЧНЫХ РАЗБИЕНИЙ ШКАЛЫ ВОЗРАСТА
Таблица 1.
|
Точки разбиения возраста на интервалы |
Значения р-статистики |
|
40 |
20.63 |
|
41 |
21.78 |
|
42 |
22.84 |
|
43 |
23.99 |
|
44 |
26.22 |
|
45 |
24.98 |
|
46 |
25.80 |
|
47 |
24.24 |
|
48 |
25.56 |
|
49 |
25.56 |
|
50 |
25.97 |
|
51 |
25.70 |
|
52 |
25.46 |
|
53 |
25.55 |
|
54 |
24.16 |
|
55 |
24.16 |
1 В скобках под значениями коэффициентов регрессии приводятся величины стандартных ошибок, позволяющие оценить доверительные интервалы.
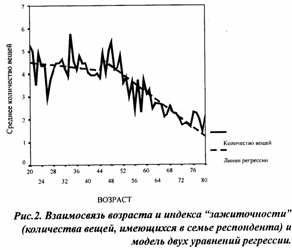
Подводя итог можно констатировать, что по сравнению с моделью, описывающей зависимость одним уравнением, перейдя к двум отдельным уравнениям, мы получили гораздо более адекватную картину. В интервале до 45 лет возраст не влияет на индекс "зажиточности", а начиная с 45 лет значение индекса падает со скоростью приблизительно "минус 1 вещь в 10 лет".
Отметим, что использование техники фиктивных (dummy) переменных позволяет не только записать полученные нами два уравнения в виде одного, но и сразу производить оценивание регрессионной модели для двух разделенных по возрасту совокупностей.
Для нашего примера регрессионное уравнение будет выглядеть следующим образом (5).
"зажиточность"=4,8 + 4,1 *D - 0,1 *D*"возраст", (5)
где D - фиктивная переменная, построенная следующим образом:
D=0 - для респондентов 20-44 лет, D=1 для респондентов 45-80 лет.
Очевидно, что уравнение (5) объединяет в рамках одной модели и уравнение (4), и тот факт, что у респондентов до 45 лет "зажиточность" от возраста не зависит и равна константе - 4,8. Полученное для модели (5) значение коэффициента детерминации R2=0,118.
Представляется, однако, что хотя запись модели в виде единого регрессионного уравнения, несомненно, удобнее, модель (5) имеет принципиальный недостаток. Получение одного значения коэффициента детерминации скрывает от нас тот факт, что для одной части опрошенных вообще нет значимой зависимости "зажиточности" от возраста, а для другой части эта зависимость есть. При таком подходе гораздо естественнее и полезнее было бы вычисление не единого R2, а отдельных значений этого коэффициента для двух возрастных совокупностей.
Гетероскедастичность
Еще одну проблему, возникающую при использовании метода регрессионного анализа по отношению к социологическим данным, высвечивает попытка изучить взаимосвязь того же индекса "зажиточности" с доходом респондента. В этом примере в качестве икса взята переменная "суммарный доход семьи респондента". Данные-тот же массив всероссийского репрезентативного опроса, проведенного ВЦИОМ в ноябре 1999 года.
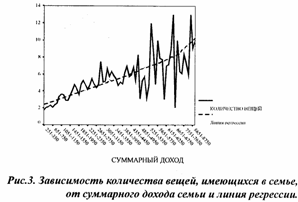
На рисунке 3 демонстрируется зависимость количества вещей в семье респондента от суммарного месячного дохода1. Построенная
1 Из анализа исключены респонденты, чей суммарный месячный доход менее 250 рублей и более 9000 рублей. Такого рода исключение является стандартной процедурой при обработке данных о доходах/расходах, когда исключаются 1-3% процента наибольших и наименьших доходов, как,либо не являющихся достоверными, либо редко встречающимися, то есть не типичными.
модель, на первый взгляд, достаточно хороша, поскольку коэффициент детерминации R2 = 0,26. Само же уравнение выглядит следующим образом:
«зажиточность»= 2,12 +0,0009 * (суммарный доход) (6)
(0,08) (0,00003)
Таким образом, с ростом дохода семьи на тысячу рублей количество вещей увеличивается приблизительно на 1. Рисунок 3 показывает, однако, что при построении регрессионного уравнения нарушается одно из ограничений метода - требование гомоскедастичности, или второе условие Гаусса-Маркова [ 1, с. 79-82].
Суть этого ограничения проста: разброс точек вокруг линии регрессии должен быть достаточно равномерен по всей протяженности линии икса. График рисунка 3 показывает, что это требование нарушено. При небольших значениях Х (то есть при невысоких размерах суммарного дохода) отклонения кривой от линии регрессии относительно невелики, но с увеличением дохода возрастают и отклонения.
Прежде всего отметим, что в тех случаях, когда в качестве зависимых переменных выступают деньги (заработок, суммарный доход и т.п.), то традиционно более эффективным является использование в регрессионном уравнении логарифма от зависимой переменной. Связано это с тем, что воздействие величины прироста (либо уменьшения) дохода на большинство социологических показателей зависит не только от величины прироста, но и от того значения, к которому этот прирост (уменьшение) происходит. Действительно, увеличение дохода на 100 рублей достаточно существенно для семей, имеющих доход в 500 рублей. И такое же увеличение (уменьшение) мало заметно для семей с доходом в 10000 рублей.
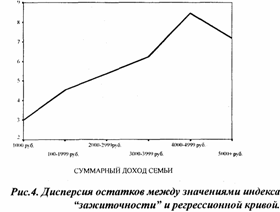
Переход к логарифму дохода вместо дохода в качестве зависимой переменной в уравнении (6) улучшает качество регрессионной модели - R2=0,3, однако принципиально ничего не меняет. Отклонения реальных значений индекса "зажиточности" от предсказываемых моделью, во-первых, остаются во многих случаях достаточно большими, и, во-вторых, эти отклонения не постоянны по оси X. На рисунке 4 показан график роста дисперсии отклонений реальных значений индекса "зажиточности" от регрессионной кривой с логарифмом суммарного дохода в качестве независимой переменной.
Если не ограничиваться визуальной констатацией нарушения требования гомоскедастичности, то можно использовать статистические тесты, которые покажут наличие/отсутствие нарушения данного ограничения. Одним из возможных тестов в данной ситуации является тест ранговой корреляции Спирмена.
Суть теста Спирмена для решения поставленной задачи достаточно проста. Ранжируются все значения Х (в нашем случае -
значения суммарного дохода), затем ранжируются все значения остатков - отклонений индекса "зажиточности" от регрессионной кривой и, наконец, выясняется вопрос о наличии взаимосвязи в расположении полученных рангов с помощью следующей статистики, называемой коэффициентом Спирмена [2, с. 48]:
![]()
Полученное для анализируемого примера значение коэффициента Спирмена равно 0,83, значимо для Р>0,999, и это подтверждает визуально установленный факт гетероскедастичности.
В качестве метода борьбы с гетероскедастичностью рекомендуется искать переменные, которые сильно связаны как с Y, так и с X. Найдя такую переменную, можно разделить на нее Х и Y и затем искать регрессию уже для этих новых переменных.
Если повезет, то новая модель будет обладать свойством гомоскедастичности. В нашем примере в качестве такого рода "компенсирующей" переменной вполне могла бы выступать характеристика "число членов семьи", которая, очевидно, сильно связана как с X, так и с Y. Социологический смысл регрессионной модели после деления Х и Y на данную переменную остается вполне прозрачным. По сути, ищется влияние среднедушевого дохода на долю индекса "зажиточности", приходящуюся на одного человека. Однако после такого преобразования модель все равно осталась гетероскедастичной.
Что означает для социолога наличие гетероскедастичности и можно ли считать модель, в которой обнаружено такое нарушение ограничений метода регрессии, хоть в чем-то пригодной? Интересно, что даже при наличии гетероскедастичности метод наименьших квадратов вычисляет оценки регрессионных коэффициентов несмещенными, то есть уравнение (6) остается корректным в части значений коэффициентов, хотя неверными становятся значения ошибок коэффициентов. Насколько велики эти ошибки, в литературе нам найти не удалось, кроме замечания, что "..дисперсия оценки коэффициента наклона может быть в три раза больше при использовании обычного МНК (метод наименьших квадратов) по сравнению с тем случаем, когда делается поправка на гетероскедастичность" [1, с. 215].
Мультиколлинеарность
Еще одной серьезной проблемой, с которой подчас приходится сталкиваться при построении регрессионных моделей в социологии, является проблема зависимости независимых переменных (то есть иксов) между собой. Напомним, что хотя классический регрессионный анализ предполагает, что иксы независимы между собой, в любых реальных приложениях оказывается, что так бывает достаточно редко. Действительно, как правило, между иксами есть корреляция, и, подчас, достаточно высокая. Само по себе это является нарушением регрессионной модели и носит название мультиколлинеарности.
При каких значениях взаимосвязи между иксами можно сказать, что мы сталкиваемся с проблемой мультиколлинеарности? В некоторых работах можно встретить рекомендации, указывающие пороговое значение как 0,7 [З]. Однако известно, что "не существует точного граничного значения уровня корреляции переменных, при котором возникает проблема мультиколлинеарности" [4, с. 290]. Рассмотрим конкретный пример, когда данная проблема возникает и какими осложнениями для социолога она чревата.
В качестве зависимой переменной будем рассматривать все тот же индекс "зажиточности". Ранее было доказано, что, впрочем, и так очевидно, что на значение этого индекса оказывает существенное влияние суммарный доход семьи. Однако вполне содержательным является и следующий социологический вопрос. Что влияет на "зажиточность" сильнее - суммарный доход или среднедушевой? Для решения этого вопроса можно построить регрессионную модель, в которой в качестве независимых переменных будут выступать два этих показателя. Для того же массива данных, полученных ВЦИОМом в ноябре 1999 года, получается следующее регрессионное уравнение (7).
"зажиточность"=2,2 + 0,001*(суммарный доход)-0,00057*(среднедушевой доход) (7) (0,08)(0,00003) (0,00014)
Коэффициент детерминации для модели (7) равен 0,27, все коэффициенты в уравнении значимы с Р>0,999. Сама модель дает вполне ожидаемый ответ на поставленный вопрос о степени важности двух рассматриваемых показателей для "зажиточности". С ростом суммарного дохода (при постоянном среднедушевом) "зажиточность" растет со скоростью "1 вещь на 1000 рублей". Иными словами, при постоянном среднедушевом доходе, то есть при одновременном увеличении суммы дохода и числа членов семьи, "зажиточность" возрастает. С другой стороны, при фиксированном суммарном доходе увеличение среднедушевого дохода ведет к уменьшению "зажиточности" со скоростью "0,6 вещи на 1000 рублей". Этот факт менее очевиден. Его можно попытаться проинтерпретировать так: при фиксированном суммарном доходе увеличение среднедушевого говорит об уменьшении размера семьи и, соответственно, в меньшей семье будет меньше вещей.
При этом уравнение (7) показывает, что положительное влияние суммарного дохода почти в 2 раза выше, чем отрицательное влияние среднедушевого дохода.
Таким образом, наша модель дала достаточно естественные, с социологической точки зрения, результаты, и можно было бы этим удовлетвориться. Однако, если взглянуть на коэффициент корреляции между суммарным и среднедушевым доходами, то он окажется весьма высоким - 0,77, и, следовательно, мы имеем дело с мультиколлинеарностью модели (7). Чем это грозит?
Основной недостаток регрессионной модели в случае мультиколлинеарности - неустойчивые значения коэффициентов модели. Мы провели численные эксперименты с формированием 100 случайных 50% подвыборок и вычислением для каждой из них моделей типа модели (7). В 38% случаев коэффициент при показателе "среднедушевой доход" давал значения 95% доверительного интервала, отличающиеся от истинного, в качестве которого у нас выступали значения коэффициента для полной выборки. Следовательно, вполне можно допустить, что и сама модель (7) с большой вероятностью даст неверные значения коэффициентов при переносе результатов на генеральную совокупность.
Подводя итог, можно сказать следующее. Современные статистические пакеты сделали техническую сторону обработки данных массовых опросов и социологических исследований весьма простой и доступной. Для того чтобы выполнить факторный, или регрессионный, или какой-либо другой анализ, достаточно несколько раз нажать на соответствующие иконки и, вроде бы, получить готовый результат. Однако на самом деле все существенно сложнее. Обработка данных, относящихся к любой предметной области, требует как знания существа и специфики методов многомерного статистического анализа, так и хорошей подготовки в самой предметной области. Продемонстрированные в статье сложности применения регрессионных моделей в социологии - только небольшой пример тех проблем, которые возникают, если серьезно подходить к анализу данных.
ЛИТЕРАТУРА
1. Доугерти К. Введение в эконометрику. М.:ИНФРА-М, 1999.
2. Глинский В.В., Иония В.Г. Статистический анализ. М.:Филинъ, 1998.
3. Lewis-Beck M. Applied Regression: An Introdaction. Sage Univer. Series Paper on Quantitative Applications in the Social Sciences, 07-022. Beverly Hills, CA:Sage.
4. Уотшем Т.Дж., Паррамоу К. Количественные методы в финансах. М.:ЮНИТИ, 1999.

 .
.